🧠 Solving Suguru Puzzles with Evolution: Building a Genetic Algorithm in Python

If you're a fan of logic puzzles like Sudoku, you’ll love Suguru, and if you're a programmer like me, you'll love solving it with code even more.

I recently built a Suguru puzzle solver using a Genetic Algorithm (GA), and in this post, I’ll walk you through what Suguru is, why it’s such a fun challenge, and how I used evolutionary principles to crack it.

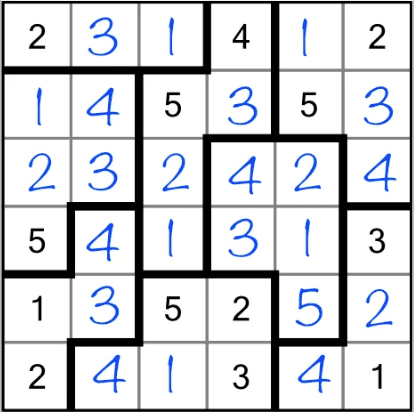
🧩 What is Suguru?

Suguru is a lesser-known logic puzzle, but don’t let that fool you, it's a beautiful brain-bender.

Each puzzle grid is divided into irregular regions.
Each region must be filled with unique numbers from 1 to n, where n is the number of cells in the region.
Adjacent cells (even across regions!) can’t share the same number.

The rules are simple, but the complexity scales fast, especially as the size of the grid grows.

Suguru example puzzle — insert image if available

🧮 Solving Suguru with Backtracking

In addition to the Genetic Algorithm solver, I also implemented a classical backtracking algorithm to solve Suguru puzzles. This approach is based on recursive depth-first search, commonly used for solving constraint satisfaction problems like Sudoku.

How It Works

The backtracking algorithm explores the puzzle grid cell by cell, trying valid number assignments while respecting Suguru's rules:

Find an empty cell in the grid.
Try all possible values from 1 to the size of the region the cell belongs to.
Check if the value is valid, meaning:
It does not repeat within the region.
It does not appear in any adjacent cells.
If valid, assign the value and move to the next empty cell.
If no value fits, backtrack by resetting the current cell and trying a different value in the previous one.

Pros & Cons

✅ Advantages:

Guarantees a correct solution (if one exists).
Simple and deterministic.
Easy to verify and debug.

❌ Limitations:

Performance degrades quickly for large or complex grids.
Does not scale well without optimizations like constraint propagation or forward checking.

When to Use It

The backtracking solver is great for:

Small to medium-sized puzzles.
Benchmarking the Genetic Algorithm.
Generating ground-truth solutions during development or testing.

🧬 Why a Genetic Algorithm?

Solving Suguru isn't trivial. Traditional techniques like backtracking work well for small puzzles, but as difficulty increases, so does the time and computational effort.

That’s where Genetic Algorithms come in.

Inspired by biological evolution, a GA doesn't try to brute-force the perfect solution. Instead, it:

Starts with a population of random solutions.
Evaluates how “fit” each solution is.
Selects the best ones to “reproduce.”
Applies crossover and mutation to generate new solutions.
Repeats this process for generations until it converges on a valid puzzle solution.

It’s not guaranteed to be perfect — but it’s often fast and effective, especially for larger or randomly generated puzzles.

🛠️ How I Built the Suguru GA Solver

You can find the full project on GitHub: 👉 luizcartolano2/suguru-ga

🧠 Under the Hood — How the Genetic Algorithm Works

The core of the solver is a Genetic Algorithm that evolves full Suguru grid candidates over generations. Each individual in the population is a complete puzzle attempt, and the algorithm aims to minimize rule violations until a valid solution is found.

🧬 Individual Representation

Each individual is represented as:

A 2D matrix of integers — the full Suguru grid.
A list of regions, where each group is a list of cell positions.
A list of fixed cells — the given clues that should never change.

To preserve puzzle constraints:

Fixed cells remain constant throughout the algorithm.
Each group must contain numbers from 1 to n, where n is the group’s size.

🎯 Fitness Function

The fitness function penalizes violations of Suguru rules. The goal is to minimize this penalty score:

+10 for each duplicate value in adjacent cells.
+10 for duplicate values within a group.
+5 for values out of the valid 1...n range in a group.
+5 for missing values in a group.

A score of 0 means a perfect, valid solution.

💡 Elitism (Keeping the Best)

To maintain stability and avoid losing good solutions, the top 10% of individuals are directly passed to the next generation. This:

Prevents regression from one generation to the next.
Helps preserve high-quality partial solutions.
Accelerates convergence toward valid answers.

🧬 Crossover

The crossover step combines traits from two parent solutions to generate offspring. Since each individual is a complete grid, we apply crossover in two domain-specific ways:

Row-wise crossover:

For each row in the new grid, randomly choose whether it comes from Parent 1 or Parent 2.

Group-wise crossover:

For each group, randomly choose whether the group’s values come from Parent 1 or Parent 2.

Each time a crossover is applied, one of these two strategies is randomly chosen. This mixed strategy ensures both global and regional patterns are preserved and recombined.

🔀 Mutation

Mutation introduces small, random changes in individuals to maintain genetic diversity and explore new solutions. Two mutation strategies are used:

Swap within a group:

Select a random group.
Randomly pick two non-fixed cells in that group.
Swap their values.

Smart mutation (constraint-aware):

Pick a group with duplicate or missing values.
Attempt to fix the group by replacing a wrong value with a correct one.

Mutations occur with a configurable probability — and finding the right mutation rate is key. Different puzzles required different settings during testing.

▶️ Getting Started

Clone the repo and install dependencies:

git clone https://github.com/luizcartolano2/suguru-ga
cd suguru-ga
pip install -r requirements.txt

Run the solver with:

python main_ga.py

Or, if you prefer classic backtracking:

python main_backtracking.py

📈 Experiments and Results

Experiments

I ran multiple experiments to compare the performance of the Genetic Algorithm against the backtracking solver. The goal was to see how quickly each method could solve various Suguru puzzles of different sizes and complexities.

I used a set of puzzles ranging from easy to hard, with varying numbers of missing cells. The puzzles were obtained from an online website that has a collection of Suguru puzzles that can be played online. A total of 240 puzzles were used for testing both algorithms.

🧮 Backtracking Results

The Backtracking Algorithm performed well on all puzzles, especially the easier ones. It solved every puzzle and took an average of 0.2 seconds per puzzle, with the highest time being 12 seconds.

At the image below, you can see the distribution of solving times for the backtracking algorithm across different puzzles. The boxplot shows that most puzzles were solved quickly, with a few outliers for more complex puzzles.

Another analysis made was the solving time vs. the number of missing cells in the puzzle. The graph below shows that as the number of missing cells increases, the solving time also increases, as expected. However, the backtracking algorithm still managed to solve all puzzles within a reasonable time frame.

🧬 Genetic Algorithm Results

The Genetic Algorithm was more variable in its performance. It solved most puzzles, 233 out of 240, but struggled with some of the harder ones, especially those with many missing cells.

As we can see in the boxplot below, the average solving time for the Genetic Algorithm was around 2 seconds, with some puzzles taking up to 30 seconds. The algorithm was generally slower than the backtracking algorithm when having too many missing cells, but it was equally fast for easier puzzles.

The graph below shows the solving time vs. the number of missing cells for the Genetic Algorithm. It shows that the solving time increases with the number of missing cells, but much more dramatically than the backtracking algorithm.

🙇‍ Discussion

In general, the Genetic Algorithm performed well on most puzzles, especially the easier ones. It was able to solve 97% of the puzzles, while the backtracking algorithm solved all of them. However, the GA took longer on average, especially for harder puzzles with many missing cells.

The results show that the GA is a viable alternative to traditional backtracking methods for solving Suguru puzzles, but it requires careful tuning of parameters like mutation rates and population size. It also highlights the trade-off between exploration and exploitation in heuristic search.

It's clear that the current implementation can be improved, especially in terms of performance and robustness. The GA could benefit from more sophisticated selection strategies, adaptive mutation rates, and better handling of edge cases.

Although the GA results were not as consistent as the backtracking algorithm, it still managed to find solutions for most puzzles, demonstrating the power of evolutionary algorithms in solving complex combinatorial problems. And future improvements could make it even more effective, so it's definitely worth exploring further.

Considering the lack of existing solutions for Suguru that are not based on backtracking in the current literature, this project is a great starting point for anyone interested in applying genetic algorithms to logic puzzles.

📊 What I Learned

This project taught me a lot about:

Designing effective fitness functions for constraint problems
Avoiding local minima by tweaking mutation rates
Balancing exploration vs. exploitation in heuristic search
And yes, debugging grid logic is way more painful than it looks

But it also gave me a deep appreciation for how evolutionary algorithms can find structure in chaos, even in something as human as a logic puzzle.

🌱 What’s Next?

Here are some ideas I want to explore:

Speed optimization and parallelization
Web-based Suguru puzzle game + solver
Integration with constraint satisfaction libraries like z3
Maybe even training a neural network to predict good initial populations?

🔗 Try It Out

The repo is fully open source, and I’d love to hear your feedback or see your PRs:

📂 GitHub – luizcartolano2/suguru-ga

💬 Final Thoughts

Whether you're a puzzle geek, an algorithm nerd, or just looking for a fun AI weekend project, give Suguru and Genetic Algorithms a try. It’s a great way to explore optimization, search strategies, and creative problem-solving.

Let me know what puzzles you solve with it!